The University of Michigan – Shanghai Jiao Tong University Joint Institute (UM-SJTU JI, JI hereafter) Associate Professor Yongxing Shen and his team have published a research article titled “An asynchronous variational integrator for the phase field approach to dynamic fracture” in International Journal for Numerical Methods in Engineering, a top journal in computational mechanics. The published research is expected to improve the computational efficiency for the phase field approach to dynamic fracture, and provide a means for further investigation of dynamic crack propagation and branching.

Figure 1. The crack patterns of dynamic fracture simulations represented as phase fields, where the region with d=0 represents the fully cracked state and that with d=1 represents the pristine state of the material.
Fracture mechanics studies crack propagation in materials and structures. Dynamic fracture refers to crack development processes accompanied by fast changes in applied loads and rapid crack propagation and generally involves bifurcation and unstable propagation of cracks. Daily live examples include cracks of the mobile phone screen due to falling, cracks within lithium batteries under impact, cracks of walls caused by earthquakes, and gas tank explosion and so on. Since crack propagation is fast and there are multiple spatial scales and multiple physical processes involved, experimental investigation is usually challenging. Hence, numerical simulation is a vital tool to study dynamic crack behaviors. Classical numerical methods solve the mechanics and crack evolution equations synchronously and is time consuming. Especially, if there are multiple material components involved, the global critical time step is restricted by the component with the fastest wave speed, causing the waste of computing resources of other components to some extent.
To improve computational efficiency for dynamic crack propagation, the research team led by Yongxing Shen adopted an asynchronous algorithm to asynchronously advance the local solution without violating causality. More precisely, a smaller time step is used in the region with a faster wave speed while a larger time step is used in the region with a slower wave speed, which saves a lot of computing resources for the latter. In addition, only one local region is solved at a time and the complicated crack equations are also effectively solved. Therefore, the proposed asynchronous method renders the computation highly efficient, which is up to 4 times faster than that of traditional synchronous methods.
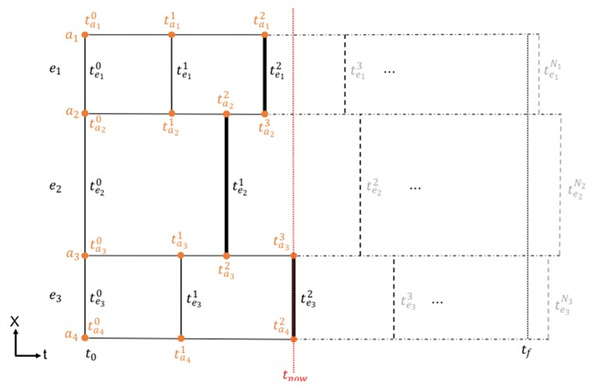
Figure 2. Asynchronous discretization of the time domain for a three-element mesh. Classical methods synchronously update all elements, while the proposed asynchronous method only updates one element at a time and the entire update schedule follows the chronological order and causality.
Yongxing Shen is the corresponding author of this paper. JI graduate student Zongwu Niu is the lead author. Other authors are former JI postdoc Vahid Ziaei-Rad (currently a researcher at Department of Environmental Informatics, Helmholtz Centre for Environmental Research – UFZ, Leipzig, Germany) and former JI undergraduate student Zongyuan Wu (currently a graduate student at Carnegie Mellon University). This research was supported by the National Natural Science Foundation of China, Grant No. 11972227 and by the Natural Science Foundation of Shanghai, Grant No. 19ZR1424200.
Personal Profile

Yongxing Shen is a tenured Associate Professor of the UM-SJTU Joint Institute, Shanghai Jiao Tong University. He received his B.S. degree from Tsinghua University in 2003, and M.Sc. and Ph.D. degrees from Stanford University in 2006 and 2008, respectively. He continued to work at Stanford University as a Postdoctoral Scholar after receiving the doctoral degree, then worked in Universitat Politecnica de Catalunya in Spain as a lecturer in 2011. He joined JI in 2014. Professor Shen’s current research interest is computational fracture mechanics. He has published more than 50 papers in journals such as International Journal for Numerical Methods in Engineering and Computer Methods in Applied Mechanics and Engineering.